This piece is a critique of a video featuring Dan Mitchell of the Cato Institute created by the Center for Freedom and Prosperity, a flat-tax lobbying group from the United States. This video was brought to our attention during a discussion about tax rates in Canada even though the video itself is discussing taxes in the USA.
Our conclusion is that this video utterly fails to demonstrate the truth of its claims, and instead relies on psychological manipulation to try to ‘win’ the argument in the minds of viewers. We believe that this group deliberately distorts and misrepresents these issues because it is their job to promote these positions regardless of their validity. As contributors to Vision of Earth and relatively informed citizens, we consider it our job to combat misinformation wherever we find it. In the following analysis we will sketch out why we believe the statements in this video to be false and misleading.
The video, available on YouTube, is called “Debunking White House Pro-Tax Increase Propaganda”.
Contents
Social Mobility
Their first criticism is levelled at the “zero-sum class warfare approach” which “assumes that people are trapped in their current level of income.” Essentially what they are saying is that the White House video is based on the idea that the United States has very limited social mobility. For those unfamiliar with the term, social mobility is the extent to which a person can change their position in the socioeconomic hierarchy. The idea of social mobility is closely connected with the concept of a meritocracy – where people rise or fall in the social hierarchy according to their skills and hard work. In essence, higher social mobility implies that a society is closer to being a meritocracy. If a society is close to a meritocracy, then a poor person is likely to become wealthy through their skills and hard work while it is also possible for a wealthy person to become poor through laziness and error.
As far as this video goes, it is not clear why they brought up social mobility in the first place. The creators of this video apparently thought it would be something they could critique in the White House’s video. Transforming the relatively straightforward discussion put forward by the White House into a discussion about social mobility is a red herring, which is a type of logical fallacy. That is, social mobility is a subject of questionable relevance to the discussion at hand. Still though, we will examine these claims carefully.
The Economic Mobility Project has come up with a set of detailed findings regarding social mobility in the United States. In the US, people have relatively little ability to climb to higher income brackets. The US has very low social mobility for the highest and lowest portions of society. Economic mobility in the states is actually falling, and is very ‘sticky’ at the ends. This means that those people who are already at either end of the income distribution are quite likely to remain there regardless of their abilities, effort, and economic choices.
The video cherry-picks statistics that seem to indicate great social mobility in America, while ignoring the greater body of statistics that suggest the contrary. They thus build a conclusion that appears to be incorrect when the real facts are studied carefully. We suggest that the reader examine literature on social mobility in the states so that they can see how deliberately misleading the video is on this point.
Reducing government to improve social mobility
“There would be even more [social mobility] if we reduced the burden of government.” This is an utterly unfounded statement that runs counter to the best facts we have available to us. A large portion of government spending goes to helping the people on the lower end of the income spectrum in the form of subsidized housing, social welfare, and other social programs. Additionally, much of government spending is spent on all citizens, regardless of income. This sort of spending includes law and order, education, physical infrastructure, national security, medicare, etc. Government acts substantially to improve social mobility through these expenditures. Statements to the contrary, such as those portrayed in this video, seem to rely on ideological reasoning, not facts.
Rising tide lifts all boats
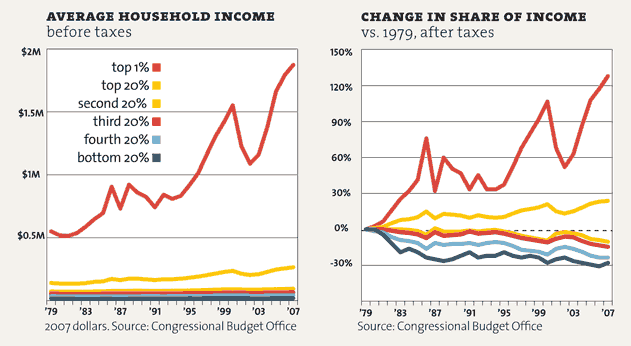
“If the pie gets larger, then everyone can have a bigger slice.” – While sounding like a truism, this is a specific framing of the economic growth discussion to make it seem like our #1 goal as a society should be expanding the economy, whatever the cost. This glosses over the fact in the past thirty years, as tax rates for the rich have declined, the share of economic growth that goes to the lower 80% of earners has stagnated.
That is, the rich have made spectacular gains in the last few decades, while the rest of the nation was left with the same amount of pie. This also glosses over the fact that the share of the working class can even shrink on a per-capita basis, even as the pie grows.
Tax cuts ARE expensive
They state that tax cuts are not expensive, this is a lie. Tax cuts can be incredibly expensive to a society. Think of municipalities that can’t upkeep roads and bridges (ie. Minneapolis) because they lack the tax income to do it. Think of the currently ballooning debt in the US, Canada, and many other nations. Every area of government investment or regulation can suffer from tax cuts. Decisions on tax structure and government expenditure must be made together. No credible claims to truth or real-world validity can be made without a full description of both sides of that equation.
They criticize the White House presentation’s viewpoint that the tax cuts are ‘costs’ for the government. This phrasing, however, is technically valid. It is often used in discussions of government tax policy. To be clear it is often stated that “tax cuts cost money”. Also, this phrasing is very appropriate at the time this video was made because the Bush-era tax cuts were slated to expire. When the tax cuts had been passed into law during the Bush administration, there had not been sufficient support to make them permanent. Very likely the taxes were thought of as a relatively temporary measure intended to get the economy rolling with a few years of theoretically higher investment from the rich. This means that the current plan was that the tax cuts for the rich would end at a predetermined time, thus taxes would increase for the rich. Government planning during the interim years would have assumed that these taxes would have returned to previous levels in 2008 – since that was the plan.
From this perspective, it is completely valid to state that new tax cuts to replace the ones that are ending would cost the government money. In this case, costs are defined as deviations from the budgetary plan as it has been laid out into the future. They have nothing to do with the government thinking that it owns 100% of everyone’s labour. This is another red herring intended to distract us from the actual discussion at hand. The speaker in this video is from the Cato Institute – a well-known right-wing libertarian think-tank. They certainly know that this is standard terminology, yet they are making a big deal out of it. We believe they are doing so because they have relatively few genuine arguments to raise on this subject, so they are instead trying to attack the White House’s video by attempting to nit-pick their language.
General attack on White House credibility
He claims that the administration has done ‘simplistic estimates’. That is almost certainly a lie considering the care and attention that the Obama administration has put into its economic policies. The Obama administration relies heavily on the knowledge of the best economists that they can find for their predictions and policy proposals. This video uses this statement as an ad hominem attack. It is an attack against the originator of an idea or statement, presented as a rebuttal of the statement itself. This is a widely used logical fallacy that is particularly common in statements from right-wing thinkers and politicians in North America. The video presents no genuine argument as to why the White House’s estimates are ‘simplistic’, thus this is purely an ad hominem attack with no basis in fact.
Laffer curve does not support their conclusions
The claims regarding simplistic estimates and the Laffer curve attempt to dodge around one of the central underlying facts about this discussion. The Obama administration obviously believes that the economy is on the left side of the Laffer curve, and/or that these tax cuts are still morally justifiable even if they might be at the top of the Laffer curve or slightly to the right. However, the location of the tax system on the Laffer curve is something that has been extensively studied by economists. So what are the answers that they have come up with?
The existing data does not agree with this video. Only the very highest tax rates, those paid by the richest people in the States, are nearly the same as some of the estimates of the Laffer peak at around 35%. We will discuss below how there is a giant difference between the marginal tax rates of around 35% and the actual tax rates paid by the rich. Regaring the Laffer peak, we suggest to the doubtful reader that they look at the empirical evidence underlying these claims that is summarized well in the Wikipedia page about the Laffer curve.
Rich don’t pay high taxes
At this point it is important to note that the richest Americans actually pay nowhere near the marginal tax rate for their tax bracket. A good illustration of this fact is this IRS report from 2007 for the 400 people who paid the most income tax that year. The richest people in the US actually only paid an average of 16.62% income tax in 2007! That is about half of the marginal tax rate for people in their income bracket. To put this into perspective, Warren Buffet popularized the fact that he pays a far lower overall tax rate (17.7%) than his secretary (30%). You can read about how Buffet criticizes the US tax system using this fact as his central point. Why is it the case that the rich pay so little? The answer is a combination of effects such as tax loopholes, capital gains, and tax breaks. The actual tax rate paid is far below the estimates of the Laffer peak for the US. Thus the argument presented in this video is invalid.
We mentioned capital gains above because it is an important factor in the low tax rates that the rich tend to enjoy. Income that can be classified as ‘capital gains’ is taxed at a much lower rate than normal income. The wealthy naturally make a lot of their money through capital gains compared to the poor or middle class because the wealthy tend to own a lot of stocks, bonds, real estate, etc. The lower tax rate on capital gains is also an incentive for the rich to reorganize their income so that as much as possible can be regarded as capital gains and not standard income.
Reagan added new taxes and closed loopholes
This video also claims that by reducing taxes in the early years of the Reagan administration, the government made way more money in taxes from the rich later in the administration. We will now discuss the truth behind this statistic, and how this video attempts to misuse this fact for its own ends.
Tax collection from the rich during the 80’s increased for many reasons. One small contributing factor is that income disparity between that highest tax bracket and the rest of the United States increased massively starting at the beginning of the Reagan era. The rich were again claiming a bigger and bigger portion of the pie.
The most important factor in the Reagan-era tax income changes for the rich appears to be the closing of tax loopholes and the creation of new taxes. The rich were hiding their money using techniques that left it untaxed, such as offshore accounts or intertwining their assets closely with corporations. In this way, they were primarily taking advantage of loopholes in the tax system. Related tactics and loopholes were, and are, used by corporations, which represent the wealth and income of their stockholders. Corporate stock tends to be concentrated in the hands of the wealthy.
The net effect of all of these changes was that many wealthy people actually paid much higher net tax rates after these changes than they had before. This video glosses over these very important facts relating to the general context of the Reagan tax changes. With this closer evaluation, the claims made in this video regarding the magical increase in the government’s tax income due to lowering of the tax rate appear to be completely false.
It is important to note that this video claims a cause-and-effect relation between lowering tax rates and corresponding increases in government income from those taxes. This claim can be true in some specific circumstances, but it definitely not true in general. We refer the reader again to the Laffer curve discussion above for details on the relationship between tax rates and government income.
Despite what Dan Mitchell might think, quoting Kennedy about tax cuts doesn’t mean he has actually made a rebuttal of any kind. This is yet another red herring and an appeal to authority.
Conclusion: This video is designed to be misleading
Overall the video fails to demonstrate the truth of its claims. Also, it deliberately misleads the viewers on a number of major points. This is certainly done deliberately, since think-tanks as well-funded as these have access to the real facts as well and have employed educated people who can understand them as well as we can. It is thus our conclusion that this video is intended to mislead the general public about these very important issues.